Понятие системы координат
Системы координат– набор правил, ставящих с соответствие некоторому объекту набор чисел.
Декартова система координат. В этой системе координат положение произвольной точки Р в пространстве задается тремя вещественными числами (координатами), обозначающими перпендикулярные проекции этой точки на три фиксированные, взаимоперпендикулярные, градуированные линии, называемые осями координат.
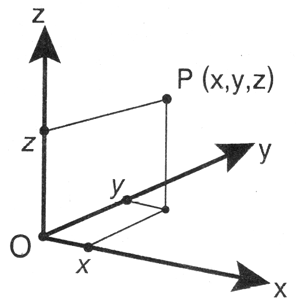
Рис. Декартова система координат.
Обычно эти три оси координат обозначаются как ось х (абсцисса), ось у (ордината) и ось z (аппликата), а отложенные на них координаты точки записываются как (х, у, z).
Точка с координатами (0, 0, 0) называется началом системы координат.
Также надо заметить, что существует два варианта таких прямоугольных систем координат: правосторонняя и левосторонняя. Чтобы разобраться в них, достаточно нарисовать на листе бумаги ось х горизонтально (положительные значения отложены справа от начала координат), а ось у вертикально (положительные значения сверху от начала координат). Теперь, если на оси z, проведенной перпендикулярно плоскости листа, положительные значения идут от листа к зрителю, то это правосторонняя система координат. В противном случае система координат — левосторонняя.
Реже, но все же достаточно часто, используются две другие системы координат: полярная цилиндрическая система координат и полярная сферическая система координат .
В цилиндрической системе координат положение точки в пространстве также описывается тремя координатами (r, 0, z):
r— это расстояние от начала координат (точки 0) до проекции точки Р на плоскость ху;
0 — это угол между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
z — расстояние от точки Р до плоскости ху.
В сферической системе координат положение точки в пространстве задается тремя координатами (r, 0, р):
r — расстояние от начала координат;
углом 0 (азимут) между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
углом р (зенит) между фиксированной полярной полуосью Oz и лучом, проведенным через начало координат (точку 0) и точку Р.
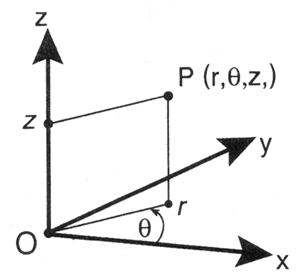

Рис. Цилиндрическая система координат Рис. Сферическая система координат
Системы однородных координат - однородным представлением n-мерного объекта является его представление в (n+1) – мерном пространстве, полученном добавлением скалярного множителя.
Пусть на плоскости заданы система прямоугольных декартовых координат по (x,y) и произвольная точка P(x,y). Любая тройка чисел (x1, x2, x3) пропорциональна тройке (x,y,1) называемой однородными координатами точки P. Если уменьшить (x,y,1) на скалярный множитель h№0, то это будут однородные координаты точки P.
Разрабатывается для описания несобственных точек пространства, для задач проективной геометрии, для записи афинных преобразований в матричной форме и для обнаружения переполнения разрядной сетки ЭВМ за счет нормализации чисел.
Глобальные и локальные СК:
1. Локальные СК – собственные координаты объектов.
2. Глобальные СК – служат для описания связей между объектами.
3. Мировая СК – входная СК в граф системах.
4. Приборная СК – для вывода на градуированное устройство.
Учебно - методический комплекс по компьютерной графике
ГАПОУ "Мензелинскийпедагогический
колледж имени Мусы Джалиля"